21.03.2014 Полосы следящих систем в Импале
Материал из SRNS
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) (→Система слежения за частотой) |
||
| Строка 16: | Строка 16: | ||
:<math>{\omega }_{k} = {\omega _{k - 1}} + \sqrt{\frac{{{S_{og}}T}}{2}}{\xi _{k - 1}}, \xi \sim N(0,\frac{{{S_{og}}T}}{2})</math>. | :<math>{\omega }_{k} = {\omega _{k - 1}} + \sqrt{\frac{{{S_{og}}T}}{2}}{\xi _{k - 1}}, \xi \sim N(0,\frac{{{S_{og}}T}}{2})</math>. | ||
| − | Результаты моделирования, полученные при параметрах <math>S_{og} = 10\ \frac{rad^3}{s^2}, T = 1\ ms </math>: | + | Результаты моделирования, полученные при параметрах <math>S_{og} = 10\ \frac{rad^3}{s^2}, T = 1\ ms </math> (соответствуют ГК-99ТК): |
<center><gallery perrow=2 widths="400px" heights="300px"> | <center><gallery perrow=2 widths="400px" heights="300px"> | ||
Версия 18:51, 22 марта 2014
Необходимо выбрать полосы систем слежения НАП Импала. На данный момент полосы предполагается задавать таблично, в зависимости от текущего отношения сигнал/шум.
Система слежения за частотой
На момент написания этой заметки, в Импале реализована ССЧ второго порядка с дискриминатором типа
.
При помощи модели системы в Matlab получены зависимости СКОш оценивания частоты от полосы системы для различных значений отношения сигнал/шум. В качестве входного воздействия подавался процесс ухода частоты опорного генератора, отвечающий модели вида:
.
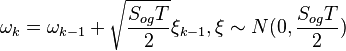Результаты моделирования, полученные при параметрах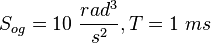 
(соответствуют ГК-99ТК):
q =30 дБГц
q =35 дБГц
q =40 дБГц
q =45 дБГц
_q_%3D30.png)
_q_%3D35.png)
_q_%3D40.png)
_q_%3D45.png)
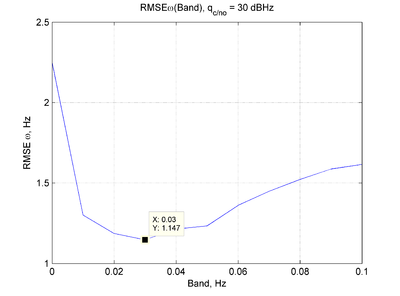
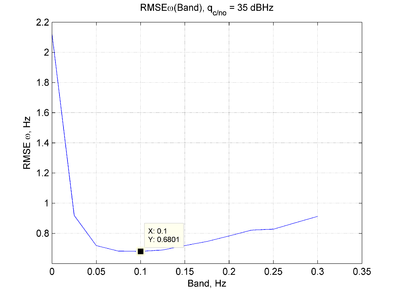
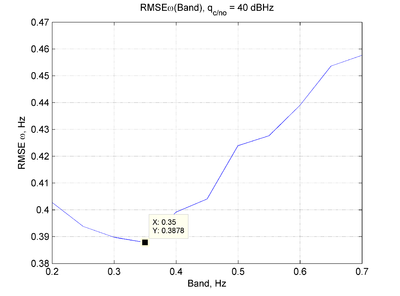
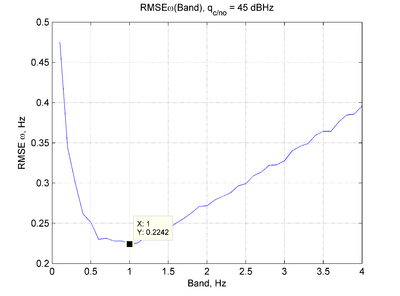
Оптимальные значения полос и соответствующие им ошибки слежения сведены в таблицу:
q, дбГц 30 35 40 45 Полоса, Гц 0.03 0.1 0.35 1 СКОш, Гц 1.14 0.68 0.38 0.22
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.