04.06.2011, Лабораторная работа по многолучевости
Korogodin (обсуждение | вклад) (→Модель многолучевого распространения сигналов) |
Korogodin (обсуждение | вклад) (→Модель многолучевого распространения сигналов) |
||
| Строка 23: | Строка 23: | ||
== Модель многолучевого распространения сигналов == | == Модель многолучевого распространения сигналов == | ||
| − | Проведем логические рассуждения, на основе которых получены математические модели многолучевого распространения, | + | Проведем логические рассуждения, на основе которых получены математические модели многолучевого распространения. |
| + | |||
| + | === Исходные данные === | ||
| + | |||
| + | Опишем Землю, отражающий экран, фазовый центр антенны навигационного спутника и фазовый центр приемной антенны НАП как сферу, ограниченный прямоугольником участок плоскости и две точки в трехмерном пространстве соответственно (см. рисунок 1). | ||
| + | |||
| + | Для этого зададим две декартовы системы координат: | ||
| + | * СК <math>x_{E}^{{}}y_{E}^{{}}z_{E}^{{}}O_{E}^{{}}</math>, связанная с центом Земли (сферы); | ||
| + | * СК <math>xyzO</math>, связанная с СК преобразованием: | ||
| + | {{ecno|1}} | ||
| + | ::<math>x=x_{E}^{{}};\begin{matrix} | ||
| + | {} \\ | ||
| + | \end{matrix}y=y_{E}^{{}};\begin{matrix} | ||
| + | {} \\ | ||
| + | \end{matrix}z=z_{E}^{{}}-R_{E}^{{}}</math>, | ||
| + | :где - средний радиус Земли, равный 6 371 км. | ||
== Домашняя подготовка == | == Домашняя подготовка == | ||
Версия 15:05, 4 июня 2011
<accesscontrol>SuperUsers</accesscontrol>
Задача: разработать методическое пособие и отработать выполнение лабораторной работы по многолучевому распространению сигналов СРНС на основе модели.
За образец оформления и стиля предлагается взять методическое пособие "МОДЕЛИРОВАНИЕ УСТРОЙСТВ ОБРАБОТКИ СИГНАЛОВ В ПРОГРАММЕ SYSTEM VIEW. Лабораторная работа № 3" авторства Сизяковой А.Ю.
Заголовок: Моделирование многолучевого распространения сигнала СРНС в среде Matlab
Содержание |
Введение
Спутниковые навигационные системы и их приложения в современном мире играют огромную роль: они способствуют развитию экономики страны, улучшают условия жизни людей, укрепляют оборону страны. Развитие навигационных технологий не останавливается: совершенствуются и космический, и наземный, и потребительский сегменты. Одна из существующих задач – повышение точности навигационных определений, одна из существующих проблем на этом пути – многолучевое распространение сигналов. Данная проблема особо остро стоит при применении навигационной аппаратуры потребителей (НАП) в условиях городской застройки, в составе военных комплексов (бронетехника, суда), при высокоточных фазовых измерениях.
Для борьбы с влиянием многолучевого распространения необходимо изучить характер этого влияния. Антенну, фронтенд и корреляторы навигационного приемника можно считать, в некотором приближении, линейными устройствами. Прохождение через них навигационного сигнала хорошо изучено. Для составления адекватной модели процессов в этих элементах приемника достаточно определить запаздывание, ослабление и фазовый сдвиг отраженного сигнала относительно прямого. Тогда в качестве модели процессов можно принять суперпозицию откликов на прямой и отраженный сигнал.
В настоящей лабораторной работе студентам предлагается развить свои представления о многолучевом распространении сигнала и его влиянии на приемник на предельно простом, но практически ценном модельном примере: приеме сигналов неподвижным приемником в условиях переотражения от вертикального экрана конечных размеров, расположенном на некотором расстоянии от приемной антенны.
Лабораторный практикум включает в себя:
- ознакомление с математической моделью многолучевого распространения и его воздействия на навигационный приемник;
- самостоятельный численный расчет отдельных зависимостей с помощью приведенной математической модели;
- моделирование многолучевого распространения сигнала СРНС в программе, созданной в среде Matlab;
- обработку и сравнение полученных результатов.
Модель многолучевого распространения сигналов
Проведем логические рассуждения, на основе которых получены математические модели многолучевого распространения.
Исходные данные
Опишем Землю, отражающий экран, фазовый центр антенны навигационного спутника и фазовый центр приемной антенны НАП как сферу, ограниченный прямоугольником участок плоскости и две точки в трехмерном пространстве соответственно (см. рисунок 1).
Для этого зададим две декартовы системы координат:
- СК
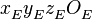, связанная с центом Земли (сферы);
- СК
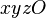, связанная с СК преобразованием:
,
- где - средний радиус Земли, равный 6 371 км.
Домашняя подготовка
Перед выполнением работ в лаборатории, обучающиеся проводят предварительную подготовку. Результаты студентами предоставляются индивидуально на бумажных носителях до начала выполнения лабораторной работы.
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.