Разработка фрагмента оптимизационной модели сенсорной радиосети (ВКР) — различия между версиями
Boldenkov (обсуждение | вклад) (Новая страница: «Научный руководитель: Губонин, Николай Сергеевич Работа предполагает изучение облас…») |
Korogodin (обсуждение | вклад) (→Рекомендуемая литература) |
||
| (не показаны 3 промежуточные версии 2 участников) | |||
| Строка 2: | Строка 2: | ||
Работа предполагает изучение областей применения, принципов построения и протоколов сенсорных радиосетей (Wireless Sensor Network – WSN). Самостоятельно под руководством научного руководителя студенту предстоит познакомиться с методами оптимизации и методами аппроксимации функций многих переменных. | Работа предполагает изучение областей применения, принципов построения и протоколов сенсорных радиосетей (Wireless Sensor Network – WSN). Самостоятельно под руководством научного руководителя студенту предстоит познакомиться с методами оптимизации и методами аппроксимации функций многих переменных. | ||
| − | Для известной математической модели оптимизации WSN определённого класса необходимо будет разработать алгоритмическую и программную реализацию (на C/C++) подсистемы мультипликативной аппроксимации многомерной диаграммы обмена 4-х показателей качества. Последнее означает следующее. Если <math>k_0,~k_1,~k_2,~k_3</math>– показатели качества WSN, причём <math>\mathbf{k}=\left(k_1,~k_2,~k_3\right)</math>, и <math>\left\{k_0(i),\mathbf{k}(i)|i= | + | Для известной математической модели оптимизации WSN определённого класса необходимо будет разработать алгоритмическую и программную реализацию (на C/C++) подсистемы мультипликативной аппроксимации многомерной диаграммы обмена 4-х показателей качества. Последнее означает следующее. Если <math>k_0,~k_1,~k_2,~k_3</math>– показатели качества WSN, причём <math>\mathbf{k}=\left(k_1,~k_2,~k_3\right)</math>, и <math>\left\{k_0(i),\mathbf{k}(i)|i=1,N\right\}</math> – результаты расчётов на оптимизационной модели WSN в <math>N</math> «точках», то необходимо построить аппроксимационную формулу вида <math>k_0=A k_1^{a_1} k_2^{a_2} k_3^{a_3}</math>, которая наилучшим образом (в смысле метода наименьших квадратов) описывает результаты расчётов. |
Работа может иметь продолжение в качестве дипломного проекта или магистерской диссертации. Желательно приступить к работе в осеннем семестре 2013/14 учебного года. | Работа может иметь продолжение в качестве дипломного проекта или магистерской диссертации. Желательно приступить к работе в осеннем семестре 2013/14 учебного года. | ||
Тема рассчитана на одного студента. | Тема рассчитана на одного студента. | ||
| − | |||
| − | |||
| − | |||
== Задание == | == Задание == | ||
| Строка 17: | Строка 14: | ||
=== Рекомендуемая литература === | === Рекомендуемая литература === | ||
| − | + | [[Категория:ВКР]] | |
| − | + | ||
| − | [[Категория: | + | |
Текущая версия на 15:21, 15 марта 2016
Научный руководитель: Губонин, Николай Сергеевич
Работа предполагает изучение областей применения, принципов построения и протоколов сенсорных радиосетей (Wireless Sensor Network – WSN). Самостоятельно под руководством научного руководителя студенту предстоит познакомиться с методами оптимизации и методами аппроксимации функций многих переменных.
Для известной математической модели оптимизации WSN определённого класса необходимо будет разработать алгоритмическую и программную реализацию (на C/C++) подсистемы мультипликативной аппроксимации многомерной диаграммы обмена 4-х показателей качества. Последнее означает следующее. Если 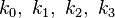 – показатели качества WSN, причём
– показатели качества WSN, причём 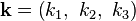 , и
, и 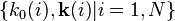 – результаты расчётов на оптимизационной модели WSN в
– результаты расчётов на оптимизационной модели WSN в 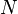 «точках», то необходимо построить аппроксимационную формулу вида
«точках», то необходимо построить аппроксимационную формулу вида 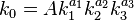 , которая наилучшим образом (в смысле метода наименьших квадратов) описывает результаты расчётов.
Работа может иметь продолжение в качестве дипломного проекта или магистерской диссертации. Желательно приступить к работе в осеннем семестре 2013/14 учебного года.
, которая наилучшим образом (в смысле метода наименьших квадратов) описывает результаты расчётов.
Работа может иметь продолжение в качестве дипломного проекта или магистерской диссертации. Желательно приступить к работе в осеннем семестре 2013/14 учебного года.
Тема рассчитана на одного студента.
Содержание |