11.12.2011, Mythbusters
Korogodin (обсуждение | вклад) (→Двухэтапная процедура поиска) |
Boldenkov (обсуждение | вклад) (→Сопоставление BOC и BPSK с позиции многолучёвости) |
||
| (не показаны 13 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | <summary>Пора разрушить парочку мифов!</summary> | + | <summary>Пора разрушить парочку мифов! <br>http://stuffpoint.com/mythbusters/image/15112-mythbusters-mr-bean-nimated-drawing.jpg </summary> |
| + | |||
| + | 2013.02.06 Обновлено: прошла защита Артёма Ожогина на тему многолучёвости. | ||
== Разрушение мифов == | == Разрушение мифов == | ||
| Строка 26: | Строка 28: | ||
Таким образом, сомнительной является ситуация "<math>2\cdot q\cdot T << 1</math>", в которой "оптимальным" является дискриминатор I*Q. Стоит ли вообще когда-либо использовать данный дискримитатор? | Таким образом, сомнительной является ситуация "<math>2\cdot q\cdot T << 1</math>", в которой "оптимальным" является дискриминатор I*Q. Стоит ли вообще когда-либо использовать данный дискримитатор? | ||
| + | |||
| + | === Дальномерные коды с "хорошими" свойствами === | ||
| + | Это идёт из связи. Для дальномерных кодов стараются подбирать псевдослучайные последовательности с низким уровнем боковых лепестков взаимно-корреляционной фукции. | ||
| + | |||
| + | Если рассмотреть набор просто случайных кодов, среднеквадратическое значение лепестков корреляционной функции будет равно <math>\frac{1}{\sqrt{N}}</math>, где N - количество символов кода на интервале накопления. Есть определённые коды, например, коды Касами, свойства которых намного лучше. Уровень боковых лепестков для кодов Касами равен <math>\frac{1}{N}</math>. | ||
| + | |||
| + | По этому поводу было сломано много копий в рамках обсуждений перспективных сигналов. На самом деле это так, но пользы от этого никакой. Все эти "хорошие" свойства остаются в силе только до тех пор, пока два сигнала совпадают по частоте. Как только появляется разность частот сигналов, свойства кодов разрушаются и становяться такими же, как и у просто наборов случайных чисел <math>\frac{1}{\sqrt{N}}</math>. Причём разность частот должна быть совсем небольшой. Если рассматривать открытые сигналы на интервале 1 мс, то при разности частот уже 50 Гц свойства кодов полностью разрушаются. А разность частот - она есть всегда. Поэтому на деле пытаться сделать дальномерные коды с "хорошими" свойствами нет смысла. | ||
| + | |||
| + | == Mythbusted == | ||
| + | http://media.tumblr.com/tumblr_li0s9igCBt1qbolbn.jpg | ||
| + | |||
| + | === Сопоставление BOC и BPSK с позиции многолучёвости === | ||
| + | Корни вопроса уходят в далёкий уже 2003 - тогда появилось множество статей по выбору сигналов для системы Galileo. (Да, я всех поздравляю, системе Galileo оказывается уже 10 лет! Вообще-то намерение появилось в 1999 году, а в 2003 году проект был официально утверждён). | ||
| + | |||
| + | В качестве основного открытого сигнала Galileo E1 рассматривался сигнал с модуляцией BOC(1, 1), который постоянно сравнивался с сигналом GPS L1 C/A, имеющим модуляцию BPSK(1). | ||
| + | |||
| + | Исследовались различные показатели, в частности, воздействие многолучёвости. В результате обилия статей сложилось впечатление, что модуляция BOC '''в принципе''' лучше, чем BPSK. | ||
| + | |||
| + | Однако подобное утверждение, без указания параметров, в общем случае не имеет смысла. Если сравнивать именно BOC(1, 1) и BPSK(1), то BOC(1, 1) окажется несколько лучше по многолучёвости. Но если сравнивать BOC(1, 1) и BPSK(2), то лучше окажется BPSK. | ||
| + | |||
| + | Так какой вид модуляции всё-таки лучше? Надо сравнивать сигналы в неких равных условиях. Но что приравнять? | ||
| + | |||
| + | Если приравнивать скорость следования символов дальномерного кода (а это важно, разве что, для поиска), то сравнивать следует BOC(1, 1) и BPSK(1). | ||
| + | |||
| + | Но более интересным представляется сравнение сигналов с одинаковой полосой. В данном случае это будут BOC(1, 1) и BPSK(2), имеющие полосу 4.092 МГц. | ||
| + | |||
| + | Сравнение данных сигналов приведено в [[media:20130207_Ожогин_ВКР.pdf|дипломной работе Артёма Ожогина]]. Основной результат очевиден по данному графику: | ||
| + | |||
| + | [[File:20130206 MP envelope.png|Огибающая многолучёвости|500px]] | ||
| + | |||
| + | При равных полосах предпочтительнее оказывается модуляция BPSK, а не BOC. | ||
=== Двухэтапная процедура поиска === | === Двухэтапная процедура поиска === | ||
| Строка 32: | Строка 65: | ||
Бытует мнение, что для ускорения процедуры поиска её можно разделить на два этапа. На первом этапе осуществлять накопление сигнала в каждой из ячейки поиска на "небольшом" времени накопления, с не очень хорошими характеристиками. В этом случае превышение порога поиска произойдёт в большом количестве ячеек, в том числе, в правильной. Выбирается некоторое количество максимумов, и уже для этих ячеек осуществляется накопление на втором этапе, на более длительном интервале накопления с хорошими вероятностными характеристиками. Т.к. количество ячеек на втором этапе меньше, общее время накопления может быть сокращено. | Бытует мнение, что для ускорения процедуры поиска её можно разделить на два этапа. На первом этапе осуществлять накопление сигнала в каждой из ячейки поиска на "небольшом" времени накопления, с не очень хорошими характеристиками. В этом случае превышение порога поиска произойдёт в большом количестве ячеек, в том числе, в правильной. Выбирается некоторое количество максимумов, и уже для этих ячеек осуществляется накопление на втором этапе, на более длительном интервале накопления с хорошими вероятностными характеристиками. Т.к. количество ячеек на втором этапе меньше, общее время накопления может быть сокращено. | ||
| − | Этот вопрос | + | Этот вопрос исследовал [[Липа И.В.|Иван Липа]] в выпускной работе. Показано, что данный подход эффективен только тогда, когда объём поиска на втором этапе относительно велик и составляет порядка 10% от полного поля поиска. Тогда можно достигнуть сокращения общего времени поиска до 3 раз. |
Однако обычно подобные алгоритмы используют, когда объём поиска на втором этапе мал и составляет несколько десятков. В этом случае эффекта от данного подхода нет практически никакого. | Однако обычно подобные алгоритмы используют, когда объём поиска на втором этапе мал и составляет несколько десятков. В этом случае эффекта от данного подхода нет практически никакого. | ||
| Строка 38: | Строка 71: | ||
Второй недостаток - "выигравшие" на первом этапе позиции идут не "по порядку" в поле поиска, а случайно. Из-за этого затруднительно на втором этапе использовать алгоритмы быстрого поиска, которые, как правило, расчитаны на анализ блока соседних позиций. | Второй недостаток - "выигравшие" на первом этапе позиции идут не "по порядку" в поле поиска, а случайно. Из-за этого затруднительно на втором этапе использовать алгоритмы быстрого поиска, которые, как правило, расчитаны на анализ блока соседних позиций. | ||
| − | + | Результат виден из данного графика: | |
| − | + | [[File:Иссл_2ступ_поиска_30дбгц_2мс.PNG|Эффективность двухэтапного метода поиска|500px]] | |
| − | + | ||
| + | Для получения максимального выигрыша объём второго этапа должен быть порядка 10% от объёма всего поля поиска. Если объём второго этапа составляет доли процента, выигрыша не будет. | ||
| + | |||
| + | Подробности здесь: [[Blog:Lipa/24.10.2011_Двухэтапный_поиск_сигналов|Двухэтапный поиск сигналов]] | ||
| − | |||
| − | |||
{{wl-publish: 2011-12-11 20:29:57 +0400 | Boldenkov }} | {{wl-publish: 2011-12-11 20:29:57 +0400 | Boldenkov }} | ||
| + | {{wl-publish: 2013-02-07 13:39:23 +0400 | Boldenkov }} | ||
Текущая версия на 21:42, 11 февраля 2013
Пора разрушить парочку мифов! 
2013.02.06 Обновлено: прошла защита Артёма Ожогина на тему многолучёвости.
Содержание |
[править] Разрушение мифов
Давно хотел поднять эту тему. В нашем деле есть множество положений, которые воспринимаются, как данность. Они либо следуют из общих соображений, либо кажутся очевидными, либо являются результатом недоведённых до конца исследований. Либо это просто заблуждения. Короче говоря, природа их различна.
Некоторые из этих положений вызывают сомнения, но пока не проведено соответствующее исследование, сомнения остаются смутными. Может быть, они и неверны. Но точку поставить надо.
Заниматься исследованиями проблем, которые актуальными в текущий момент не являются, никто не будет. А когда появляется время, о них никто не помнит. Поэтому такие положения годами остаются "повисшими и воздухе".
Предлагаю вести список таких "подозрительных" положений и, при случае, разбираться в них. Если о проблеме никто не помнит, никто её не решит. Беда в том, что о проблеме всегда вспоминают, когда полно других дел.
Разрешение данных проблем можно доверить студентам в качестве работ - польза будет для всех. И такой пример уже есть - Иван Липа сейчас исследует двухэтапную процедуру поиска, подробности ниже.
Прошу присоединяться, "мифов для разрушения" вокруг существует большое количество.
[править] Список "для затравки"
[править] Дискриминаторы: I*Q или sign(I)*Q
Общепринято, что при большом отношении сигнал шум можно использовать дискриминатор sign(I)*Q, а при малом - I*Q.
Корни этого положения растут из оптимального синтеза. Оптимальный синтез алгоритма слежения за фазой даёт дискриминатор th(I)*Q, где th(X) - гипертангенс. Форма функции гипертангенса такова, что если аргумент очень большой (X >> 1), то он похож на знаковую функцию: 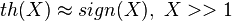 . Если аргумент очень мал (много меньше единицы), то функция гипертангенса имеет единичную производную, тогда
. Если аргумент очень мал (много меньше единицы), то функция гипертангенса имеет единичную производную, тогда  .
.
Так как систематическая составляющая на выходе коррелятора пропорциональна отношению сигнал/шум, и возникло положение, что при малом отношении следует использовать дискриминатор I*Q, а при большом отношении sign(I)*Q.
Вопрос в том, насколько мало или велико отношение сигнал/шум, о котором идёт речь. Систематическая составляющая на выходе коррелятора упрощённо имеет вид ![M[I] = 2\cdot q\cdot T cos(\Delta\varphi)](/images/math/d/3/1/d311d777139cbdec6a5ac489011e3fc1.png) . Если сопоставить данную величину с единицей, то получим:
. Если сопоставить данную величину с единицей, то получим: 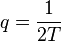 . При времени накопления 1 мс q будет равно 26 дБГц, что ещё является реальной областью работы ФАП. Однако при столь низком отношении обычно используется более длительное время накопления сигнала в корреляторе. Если взять 20 мс, то величина q будет равна 14 дБГц, что уже совсем мало для ФАП. ФАП нет смысла использовать при таком отношении, т.к. выделить данные всё равно будет невозможно.
. При времени накопления 1 мс q будет равно 26 дБГц, что ещё является реальной областью работы ФАП. Однако при столь низком отношении обычно используется более длительное время накопления сигнала в корреляторе. Если взять 20 мс, то величина q будет равна 14 дБГц, что уже совсем мало для ФАП. ФАП нет смысла использовать при таком отношении, т.к. выделить данные всё равно будет невозможно.
Таким образом, сомнительной является ситуация "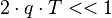 ", в которой "оптимальным" является дискриминатор I*Q. Стоит ли вообще когда-либо использовать данный дискримитатор?
", в которой "оптимальным" является дискриминатор I*Q. Стоит ли вообще когда-либо использовать данный дискримитатор?
[править] Дальномерные коды с "хорошими" свойствами
Это идёт из связи. Для дальномерных кодов стараются подбирать псевдослучайные последовательности с низким уровнем боковых лепестков взаимно-корреляционной фукции.
Если рассмотреть набор просто случайных кодов, среднеквадратическое значение лепестков корреляционной функции будет равно 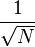 , где N - количество символов кода на интервале накопления. Есть определённые коды, например, коды Касами, свойства которых намного лучше. Уровень боковых лепестков для кодов Касами равен
, где N - количество символов кода на интервале накопления. Есть определённые коды, например, коды Касами, свойства которых намного лучше. Уровень боковых лепестков для кодов Касами равен 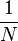 .
.
По этому поводу было сломано много копий в рамках обсуждений перспективных сигналов. На самом деле это так, но пользы от этого никакой. Все эти "хорошие" свойства остаются в силе только до тех пор, пока два сигнала совпадают по частоте. Как только появляется разность частот сигналов, свойства кодов разрушаются и становяться такими же, как и у просто наборов случайных чисел 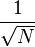 . Причём разность частот должна быть совсем небольшой. Если рассматривать открытые сигналы на интервале 1 мс, то при разности частот уже 50 Гц свойства кодов полностью разрушаются. А разность частот - она есть всегда. Поэтому на деле пытаться сделать дальномерные коды с "хорошими" свойствами нет смысла.
. Причём разность частот должна быть совсем небольшой. Если рассматривать открытые сигналы на интервале 1 мс, то при разности частот уже 50 Гц свойства кодов полностью разрушаются. А разность частот - она есть всегда. Поэтому на деле пытаться сделать дальномерные коды с "хорошими" свойствами нет смысла.
[править] Mythbusted

[править] Сопоставление BOC и BPSK с позиции многолучёвости
Корни вопроса уходят в далёкий уже 2003 - тогда появилось множество статей по выбору сигналов для системы Galileo. (Да, я всех поздравляю, системе Galileo оказывается уже 10 лет! Вообще-то намерение появилось в 1999 году, а в 2003 году проект был официально утверждён).
В качестве основного открытого сигнала Galileo E1 рассматривался сигнал с модуляцией BOC(1, 1), который постоянно сравнивался с сигналом GPS L1 C/A, имеющим модуляцию BPSK(1).
Исследовались различные показатели, в частности, воздействие многолучёвости. В результате обилия статей сложилось впечатление, что модуляция BOC в принципе лучше, чем BPSK.
Однако подобное утверждение, без указания параметров, в общем случае не имеет смысла. Если сравнивать именно BOC(1, 1) и BPSK(1), то BOC(1, 1) окажется несколько лучше по многолучёвости. Но если сравнивать BOC(1, 1) и BPSK(2), то лучше окажется BPSK.
Так какой вид модуляции всё-таки лучше? Надо сравнивать сигналы в неких равных условиях. Но что приравнять?
Если приравнивать скорость следования символов дальномерного кода (а это важно, разве что, для поиска), то сравнивать следует BOC(1, 1) и BPSK(1).
Но более интересным представляется сравнение сигналов с одинаковой полосой. В данном случае это будут BOC(1, 1) и BPSK(2), имеющие полосу 4.092 МГц.
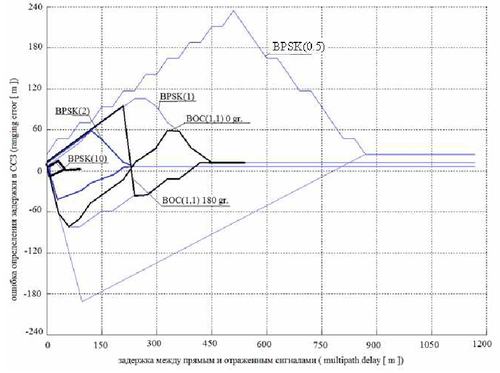
Сравнение данных сигналов приведено в дипломной работе Артёма Ожогина. Основной результат очевиден по данному графику:
При равных полосах предпочтительнее оказывается модуляция BPSK, а не BOC.
[править] Двухэтапная процедура поиска
Поиск сигнала малого уровня требует большой длительности накопления в каждой ячейке анализа. Снижение времени накопления ухудшает вероятностные характеристики, но, зато, сокращает время всего поиска.
Бытует мнение, что для ускорения процедуры поиска её можно разделить на два этапа. На первом этапе осуществлять накопление сигнала в каждой из ячейки поиска на "небольшом" времени накопления, с не очень хорошими характеристиками. В этом случае превышение порога поиска произойдёт в большом количестве ячеек, в том числе, в правильной. Выбирается некоторое количество максимумов, и уже для этих ячеек осуществляется накопление на втором этапе, на более длительном интервале накопления с хорошими вероятностными характеристиками. Т.к. количество ячеек на втором этапе меньше, общее время накопления может быть сокращено.
Этот вопрос исследовал Иван Липа в выпускной работе. Показано, что данный подход эффективен только тогда, когда объём поиска на втором этапе относительно велик и составляет порядка 10% от полного поля поиска. Тогда можно достигнуть сокращения общего времени поиска до 3 раз.
Однако обычно подобные алгоритмы используют, когда объём поиска на втором этапе мал и составляет несколько десятков. В этом случае эффекта от данного подхода нет практически никакого.
Второй недостаток - "выигравшие" на первом этапе позиции идут не "по порядку" в поле поиска, а случайно. Из-за этого затруднительно на втором этапе использовать алгоритмы быстрого поиска, которые, как правило, расчитаны на анализ блока соседних позиций.
Результат виден из данного графика:
convert: no images defined `/tmp/transform_4d558ea93b46-1.png' @ error/convert.c/ConvertImageCommand/3044.
Для получения максимального выигрыша объём второго этапа должен быть порядка 10% от объёма всего поля поиска. Если объём второго этапа составляет доли процента, выигрыша не будет.
Подробности здесь: Двухэтапный поиск сигналов
[ Хронологический вид ]Комментарии
По поводу кодов. Построить бы график перехода 1/N в 1/sqrt(N) как функции ошибки по доплеру. Ведь 50Гц при хорошей энергетике - это очень много. Что будет при 1-5 Гц?
50 Гц - это не ошибка слежения за сигналом. Это разность частот принимаемого сигнала и другого сигнала из той же системы, который создаёт внутрисистемную помеху. Частоты этих сигналов могут отличаться независимо от энергетики. Это определяется взаимным движением спутников и положением потребителя. Графики такие я строил, у меня сейчас просто под рукой его нет.
Понял)) Что-то я чушь сказал, какие 1/N в режиме слежения)
Войдите, чтобы комментировать.