28.11.2013 Формирование произвольных сигналов с помощью Waveform

Материал из SRNS
Перейти к: навигация, поиск
(Новая страница: «Радиосигналы можно представить в виде произведения двух процессов: низкочастотного экв…»)
 
Строка 1: Строка 1:
−
Радиосигналы можно представить в виде произведения двух процессов: низкочастотного эквивалента (baseband signal) и несущей гармоники (radio frequency). На этом принципе основаны векторные генераторы сигналов. Они умножают квадратуры <math>I</math> и <math>Q</math>, задающие комплексный низкочастотный сигнал, и гармоническое колебание несущей частоты.
+
<summary [ hidden ]>В векторных генераторах Rohde&Schwarz для задания низкочастотного эквивалента сигнала используются Waveform-файлы (расширение .wv). До настоящего времени их формат оставался нам неизвестным, отсутствовала программа формирования. Эта заметка должна исправить сложившуюся ситуацию.</summary>
  
−
Полоса сигнала редко превышает десятки мегагерц, а значит и спектр низкочастотного эквивалента относительно узок. Узок настолько, что низкочастотный эквивалент (то есть квадратуры <math>I</math> и <math>Q</math>) может воспроизводится цифровыми устройствами, т.к. современные ЦАП обладают полосой в сотни мегагерц.  
+
Радиосигналы можно рассматривать как произведения двух процессов: низкочастотного эквивалента (''baseband signal'') и несущей гармоники (''radio frequency''). На этом принципе основаны векторные генераторы сигналов. Они умножают квадратуры <math>I</math> и <math>Q</math>, задающие комплексный низкочастотный сигнал, и гармоническое колебание несущей частоты.
  
−
Векторные генераторы могут использовать произвольные последовательности квадратур, а значит и формировать произвольные сигналы. Ограничения лишь в полосе сигналов и их периоде.
+
Полоса сигнала редко превышает десятки мегагерц, а значит и спектр низкочастотного эквивалента относительно узок. Узок настолько, что квадратуры <math>I</math> и <math>Q</math> могут воспроизводится цифровыми устройствами, т.к. современные ЦАП обладают полосой в сотни мегагерц.
 +
 
 +
Векторные генераторы могут использовать произвольные последовательности квадратур, а значит и формировать произвольные сигналы. Остается ограничение в ''полосе сигналов'' и их ''длительности (периоде)''. Так, например, генератор [[R%26S_SMBV100A_S/N_257721_(прибор)|R&S SMBV100A 257721]] может создавать сигналы с полосой до 120 МГц и длительностью (периодом) до 256 миллионов отсчетов квадратур.
 +
 
 +
В векторных генераторах Rohde&Schwarz для задания низкочастотного эквивалента сигнала используются Waveform-файлы (расширение .wv). До настоящего времени их формат оставался нам неизвестным, отсутствовала программа формирования. Эта заметка должна исправить сложившуюся ситуацию.
 +
 
 +
 
 +
== Формат Waveform-файла ==
 +
 
 +
Формат был восстановлен по образцу Waveform'а, поставляемого с программой WinIQSim. Файл называется <code>ArbMccwDummy.wv</code>, содержит 100 точек одного периода комплексной гармоники частоты 1 кГц. Проиллюстрируем формат на примере этого файла.
 +
 
 +
Файл в HEX'редакторе:
 +
[[file:2013_MccwHex.png|center]]
 +
 
 +
Файл состоит из нескольких полей, ограниченных фигурными скобками:
 +
* Тип
 +
 
 +
Формат: <code>{TYPE:SMU-WV}</code>
 +
 
 +
Есть предположение, что исторически Waveform-файлы создавались для векторных генераторов серии SMU, отсюда и такое значение поля. Waveform-файлы с другими полями пока не наблюдались.
 +
 
 +
* Копирайт
 +
 
 +
Формат: <code>{COPYRIGHT:2003 Rohde&Schwarz SMU}</code>
 +
 
 +
* Дата создания файла
 +
 
 +
Формат: <code>{DATE:2008-10-21;16:08:33}</code>
 +
 
 +
* Постоянные слагаемые при квадратурах (предположительно)
 +
 
 +
Формат: <code>{LEVEL OFFS:0.0,0.0}</code>
 +
 
 +
* Число отсчетов низкочастотного эквивалента сигнала
 +
 
 +
Формат: <code>{SAMPLES:100}</code>
 +
 
 +
Максимальное число отсчетов, предположительно, ограничено объемом памяти генератора.
 +
 
 +
* Частота дискретизации низкочастотного эквивалента сигнала, Гц
 +
 
 +
Формат: <code>{CLOCK:100000}</code>
 +
 
 +
Максимальная частота, предположительно, ограничена генератором (полосой). Есть и ограничение снизу. Например, файл со 100 отсчетами на генераторе серии SMBV не удалось запустить с частотой дискретизации меньше 400 Гц.
 +
 
 +
* Последовательность квадратур
 +
 
 +
Формат: <code>{WAVEFORM-401:#<math>I_1Q_1I_2Q_2...I_NQ_N</math>}</code>, где <math>I_n</math> и т.д. - отчет квадратурной компоненты в формате <code>little endian int16</code>, а 401 - это, предположительно, число байт от ":" до "}", т.е. <math>4N + 1</math>.
 +
 
 +
Приведенный файл можно прочитать с помощью matlab-скрипта:
 +
<source lang=matlab>
 +
filename = 'ArbMccwDummy.wv';
 +
fid = fopen(filename, 'r+');
 +
 
 +
for i = 1:135
 +
    ch(i) = fread(fid, 1, 'char');
 +
end
 +
 
 +
for i = 1:100
 +
%    I2(i) = fread(fid, 1, 'uint8');
 +
%    I1(i) = fread(fid, 1, 'int8');
 +
%    I(i) = I1(i)*2^8 + I2(i) + sign(I1(i)); 
 +
% 
 +
%    Q2(i) = fread(fid, 1, 'ubit8');
 +
%    Q1(i) = fread(fid, 1, 'int8');
 +
%    Q(i) = Q1(i)*2^8 + Q2(i) + sign(Q1(i));
 +
I(i) = fread(fid, 1, 'int16', 'ieee-le');
 +
Q(i) = fread(fid, 1, 'int16', 'ieee-le');
 +
end
 +
 
 +
ch(i+1) = fread(fid, 1, 'char');
 +
fclose(fid);
 +
 
 +
figure(1)
 +
cost = 2^15*cos(2*pi*(0:(length(I)-1)) / 100);
 +
sint = 2^15*sin(2*pi*(0:(length(I)-1)) / 100);
 +
plot(1:length(I), [I; Q; cost; sint]);
 +
xlabel('n')
 +
ylabel('I, Q')
 +
 
 +
 
 +
figure(2)
 +
plot(1:length(I), Q - cost);
 +
xlabel('n')
 +
ylabel('Q_{file} - Q_{theor}');
 +
</source>
 +
 
 +
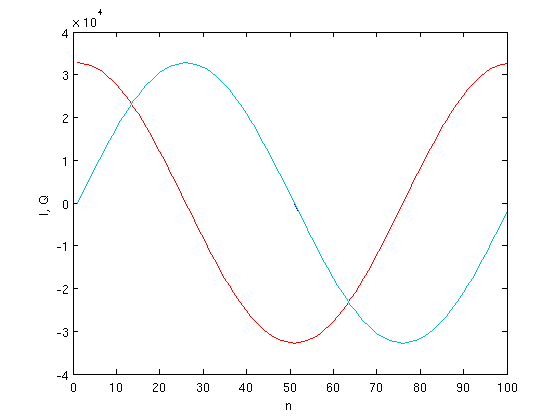
Скрипт строит графики квадратурных компонент (считанных из файла и ожидаемых, сформированных теоретически):
 +
[[file:2013_IQ_waveform.png|center]]
 +
 
 +
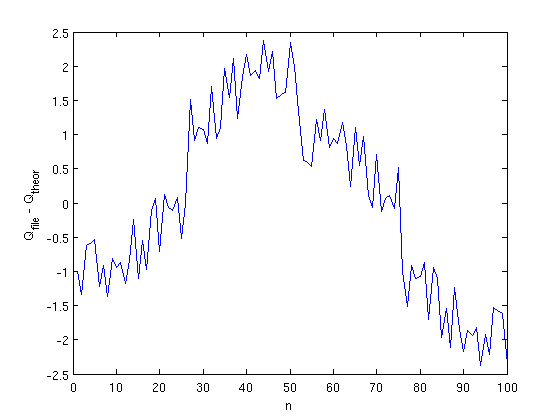
и разницы между ожидаемой и полученной квадратурой:
 +
[[file:2013_QQ_waveform.png|center]]
 +
 
 +
В целом, ожидания совпадают с полученными результатами, за исключением величины ошибки. Она превышает младший разряд (единицу) при отрицательных значениях квадратуры. Есть предположение, что немного некорректно происходит интерпретация доп.кода.
 +
 
 +
== Формирование Waveform-файла ==
 +
 
 +
Сформируем экзотический сигнал - радиопилу. Код скрипта:
 +
<source lang=matlab>
 +
filename = 'wave.wv';
 +
fid = fopen(filename, 'w+');
 +
 
 +
fprintf(fid, '{TYPE:SMU-WV}{COPYRIGHT:2003 Rohde&Schwarz SMU}{DATE:2008-10-21;16:08:33}{LEVEL OFFS:0.0,0.0}{SAMPLES:100}{CLOCK:100000}{WAVEFORM-401:#');
 +
 
 +
for i = 1:100
 +
    I = i/100 * 2^15;
 +
    Q = 0;
 +
    fwrite(fid, I, 'int16', 'ieee-le');
 +
    fwrite(fid, Q, 'int16', 'ieee-le');
 +
end
 +
 
 +
fprintf(fid, '}');
 +
 
 +
fclose(fid);
 +
</source>
 +
 
 +
HEX-полученного файла:
 +
[[file:2013_WaveHex.png|center]]
 +
 
 +
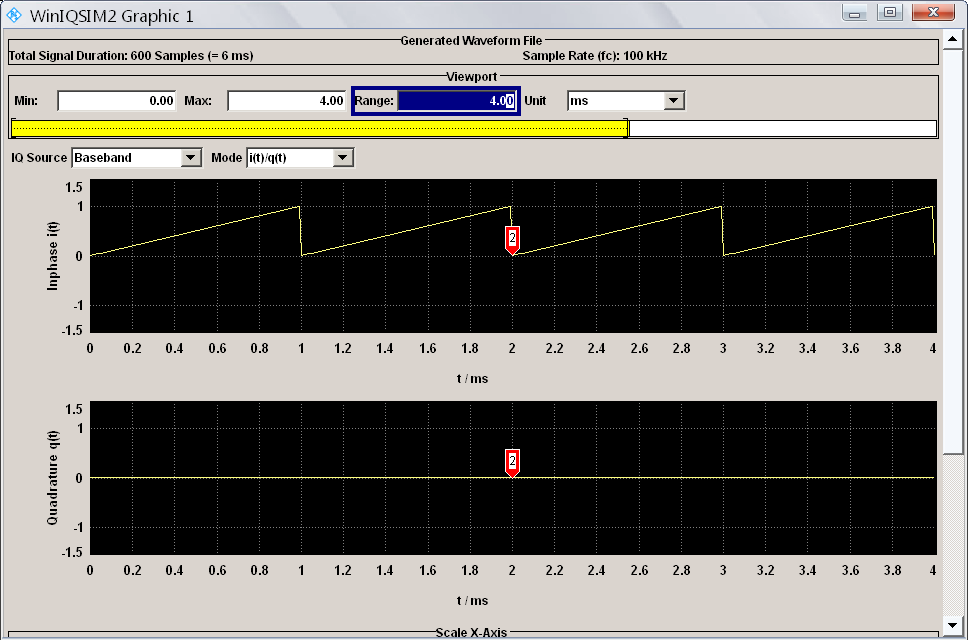
WinIQSim принимает файл без возражений:
 +
[[file:2013_WinIQSimPila.png|center]]
 +
 
 +
Есть некоторое недопонимание почему встроенный вьювер считает, что нельзя засемплировать выборку более 6 раз. Но так он себя ведет и с файлом-примером. Вероятно, ограничение в ПО.
 +
 
 +
Файл был применен на [[R&S SMBV100A S/N 256433 (прибор)|SMBV100A 256433]] ''(Baseband -> ARB -> Waveform file)''.
 +
 
 +
Выход I генератора (заодно узнали, что выход I с чертой - инвертированный I):

Версия 09:55, 29 ноября 2013

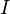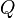Радиосигналы можно рассматривать как произведения двух процессов: низкочастотного эквивалента (baseband signal) и несущей гармоники (radio frequency). На этом принципе основаны векторные генераторы сигналов. Они умножают квадратуры I и Q, задающие комплексный низкочастотный сигнал, и гармоническое колебание несущей частоты.

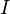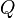Полоса сигнала редко превышает десятки мегагерц, а значит и спектр низкочастотного эквивалента относительно узок. Узок настолько, что квадратуры I и Q могут воспроизводится цифровыми устройствами, т.к. современные ЦАП обладают полосой в сотни мегагерц.

Векторные генераторы могут использовать произвольные последовательности квадратур, а значит и формировать произвольные сигналы. Остается ограничение в полосе сигналов и их длительности (периоде). Так, например, генератор R&S SMBV100A 257721 может создавать сигналы с полосой до 120 МГц и длительностью (периодом) до 256 миллионов отсчетов квадратур.

В векторных генераторах Rohde&Schwarz для задания низкочастотного эквивалента сигнала используются Waveform-файлы (расширение .wv). До настоящего времени их формат оставался нам неизвестным, отсутствовала программа формирования. Эта заметка должна исправить сложившуюся ситуацию.


Формат Waveform-файла

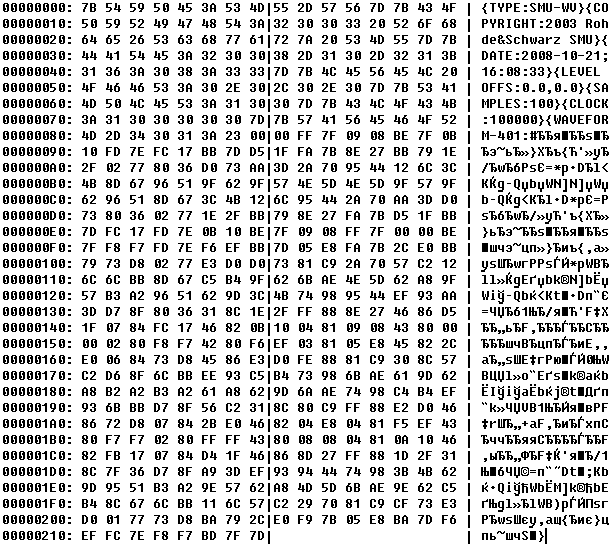
Формат был восстановлен по образцу Waveform'а, поставляемого с программой WinIQSim. Файл называется ArbMccwDummy.wv, содержит 100 точек одного периода комплексной гармоники частоты 1 кГц. Проиллюстрируем формат на примере этого файла.

Файл в HEX'редакторе:

2013 MccwHex.png

Файл состоит из нескольких полей, ограниченных фигурными скобками:

  • Тип

Формат: {TYPE:SMU-WV}

Есть предположение, что исторически Waveform-файлы создавались для векторных генераторов серии SMU, отсюда и такое значение поля. Waveform-файлы с другими полями пока не наблюдались.

  • Копирайт

Формат: {COPYRIGHT:2003 Rohde&Schwarz SMU}

  • Дата создания файла

Формат: {DATE:2008-10-21;16:08:33}

  • Постоянные слагаемые при квадратурах (предположительно)

Формат: {LEVEL OFFS:0.0,0.0}

  • Число отсчетов низкочастотного эквивалента сигнала

Формат: {SAMPLES:100}

Максимальное число отсчетов, предположительно, ограничено объемом памяти генератора.

  • Частота дискретизации низкочастотного эквивалента сигнала, Гц

Формат: {CLOCK:100000}

Максимальная частота, предположительно, ограничена генератором (полосой). Есть и ограничение снизу. Например, файл со 100 отсчетами на генераторе серии SMBV не удалось запустить с частотой дискретизации меньше 400 Гц.

  • Последовательность квадратур

Формат: {WAVEFORM-401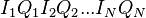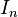:#I_1Q_1I_2Q_2...I_NQ_N}, где I_n и т.д. - отчет квадратурной компоненты в формате little endian int16, а 401 - это, предположительно, число байт от ":" до "}", т.е. 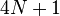4N + 1.

Приведенный файл можно прочитать с помощью matlab-скрипта:

filename = 'ArbMccwDummy.wv';
fid = fopen(filename, 'r+');

for i = 1:135
    ch(i) = fread(fid, 1, 'char');
end

for i = 1:100
%     I2(i) = fread(fid, 1, 'uint8');
%     I1(i) = fread(fid, 1, 'int8');
%     I(i) = I1(i)*2^8 + I2(i) + sign(I1(i));  
%  
%     Q2(i) = fread(fid, 1, 'ubit8');
%     Q1(i) = fread(fid, 1, 'int8');
%     Q(i) = Q1(i)*2^8 + Q2(i) + sign(Q1(i));
I(i) = fread(fid, 1, 'int16', 'ieee-le');
Q(i) = fread(fid, 1, 'int16', 'ieee-le');
end

ch(i+1) = fread(fid, 1, 'char');
fclose(fid);

figure(1)
cost = 2^15*cos(2*pi*(0:(length(I)-1)) / 100);
sint = 2^15*sin(2*pi*(0:(length(I)-1)) / 100);
plot(1:length(I), [I; Q; cost; sint]);
xlabel('n')
ylabel('I, Q')


figure(2)
plot(1:length(I), Q - cost);
xlabel('n')
ylabel('Q_{file} - Q_{theor}');

Скрипт строит графики квадратурных компонент (считанных из файла и ожидаемых, сформированных теоретически):

2013 IQ waveform.png

и разницы между ожидаемой и полученной квадратурой:

2013 QQ waveform.png

В целом, ожидания совпадают с полученными результатами, за исключением величины ошибки. Она превышает младший разряд (единицу) при отрицательных значениях квадратуры. Есть предположение, что немного некорректно происходит интерпретация доп.кода.

Формирование Waveform-файла

Сформируем экзотический сигнал - радиопилу. Код скрипта:

filename = 'wave.wv';
fid = fopen(filename, 'w+');

fprintf(fid, '{TYPE:SMU-WV}{COPYRIGHT:2003 Rohde&Schwarz SMU}{DATE:2008-10-21;16:08:33}{LEVEL OFFS:0.0,0.0}{SAMPLES:100}{CLOCK:100000}{WAVEFORM-401:#');

for i = 1:100
    I = i/100 * 2^15;
    Q = 0;
    fwrite(fid, I, 'int16', 'ieee-le');
    fwrite(fid, Q, 'int16', 'ieee-le');
end

fprintf(fid, '}');

fclose(fid);

HEX-полученного файла:

2013 WaveHex.png

WinIQSim принимает файл без возражений:

2013 WinIQSimPila.png

Есть некоторое недопонимание почему встроенный вьювер считает, что нельзя засемплировать выборку более 6 раз. Но так он себя ведет и с файлом-примером. Вероятно, ограничение в ПО.

Файл был применен на SMBV100A 256433 (Baseband -> ARB -> Waveform file).

Выход I генератора (заодно узнали, что выход I с чертой - инвертированный I):

— Корогодин Илья • 10:06, 29 ноября 2013 • нет комментариев

[ Хронологический вид ]Комментарии

< pre > Мысли движутся в сторону интересного проявления эффекта Гиббса < /pre > ...скорее в сторону ресемплера

— Шатилов Александр • 29 декабря 2013 в 19:43

Войдите, чтобы комментировать.

Источник — «https://acik.srns.ru/index.php?title=Blog:Korogodin/28.11.2013_Формирование_произвольных_сигналов_с_помощью_Waveform&oldid=10172»
Персональные инструменты
Пространства имён

Варианты
Действия
SRNS Wiki
Рабочие журналы
Приватный файлсервер
QNAP Сервер
Инструменты